This is primarily a textbook for the first course of undergraduate mathematical modeling. However, many of its R codes, as well as their Python counterparts, and modeling methods can be useful research tools in natural sciences, engineering, social sciences, and applied mathematics.
The book is based on the lecture notes I developed for an upper division course “Math 336: Introduction to Mathematical Modeling” at San Diego State University since 2015. The mathematical prerequisites for this course are a semester of calculus and a semester of linear algebra. The book includes the following topics: dimensional analysis, R programming, principles of 5-step mathematical modeling, linear regression models, linear algebra models, probability models, calculus models, stochastic models, statistical inference, big data models, machine learning models, artificial intelligence models, network models, Rgraphics models, and principles of applied mathematics consulting. The 5-step recipe of mathematical modeling process is repeatedly presented in different examples to enable readers to apply the method to practical problems. Numerous R codes are provided for analyzing big datasets, plotting maps, and visualizing space-time data, and can be directlyused for solving practical problems.
R codes are included in the book, yet computer programming experience is not required for reading this book. An R programming tutorial is described in the book and taught in class from beginning, and is the official computer program language for the course. R and R Studio are free for public download and can be installed easily for either PC or Mac.
Both R and Python codes will be made available at the future book website https://mathmodel.sdsu.edu.
Then, what is mathematical modeling? What is a mathematical model? Mathematical model is a mathematical expression, often a formula or an equation, that describes a phenomenon, such as the free-fall of an object from a height. The distance between of the object and its initial release position is modeled by (1 / 2) gt² , where g is the gravitational acceleration and t is the time from the release. Science history implies that Galileo Galilei (1564-1642) was the first who invented this formula. He designed a very smart experiment for this. At that time, it was hard to observe the free fall time t since a body falls down very fast in the free fall environment. He slowed down the free fall by a free roll of a ball on a plate with ticks (see Fig. 0.1). He placed a wire on the plate so that the ball would make a click sound when the ball rolled over the wire. He adjusted the positions of the four wires so that the ball would make click sound in uniform time intervals. He then discovered that the distance after each click sound is
where α = gsinθ and θ is the angle between the plate and the horizontal plane. The four lines' distances from the releasing points are thus
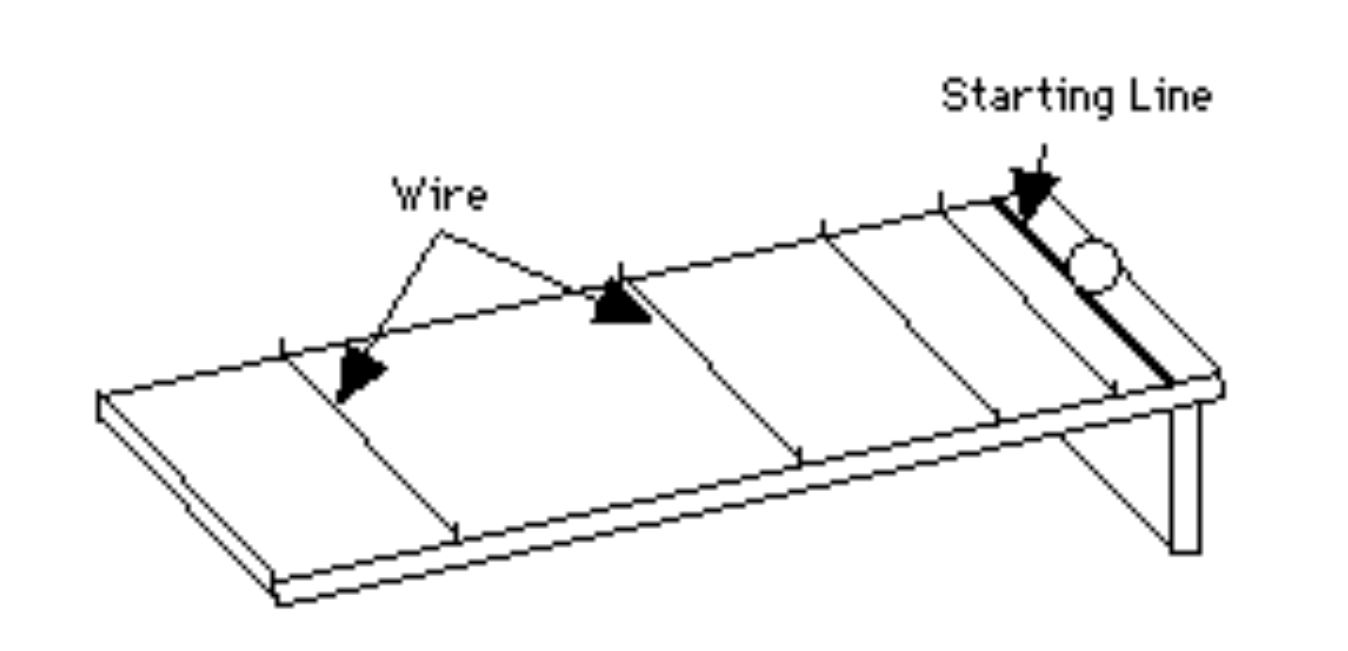
The formula s = (1 / 2)αt² is a mathematical model for the ball rolling down on a plate under gravity. Because of measurement errors, the model is not 100% accurate when compared with the observed data of time and distance. The real world problem is often that when a certain phenomenon is observed, a mathematical model is needed to describe the phenomenon in a quantitative fashion, as accurately as one can. Because observations are necessarily involved in most natural and engineering phenomena, the observational records, called observed data, are often used to develop a mathematical model. Linear regression is a commonly used approach to develop a mathematical model. This is an induction approach, deriving a mathematical model based upon data.
However, some mathematical models can be established from mathematical point of view, whose results are thought to be physically meaningful and to describe the nature. Dimensional analysis is a good approach to develop a mathematical model, such as the problem of an object’s free fall. This dimensional way is a deduction approach, which discover a mathematical model based on mathematical logic and the intrinsic relationships among the variables of the problem. Observational data are still needed to validate the model or to determine one or more critical free parameters of the model.
Both induction and deduction approaches demonstrate the power and beauty of mathematics. This book attempts to show the effectiveness, power, and wide applications of mathematical modeling, using an updated modern approach. The book covers current and future mathematical topics, such as big data, machine learning (ML), networks, artificial intelligence (AI), mathematical consulting, and R and Python programming and graphics, which are not covered in most of the existing mathematical modeling texts, but these topics are very important in the big data and AI era.
The book has another unique characteristics of interdisciplinary approach that uses calculus, linear algebra, statistics, and computing as an integrated tool to solve a practical problem, such as the analysis of spatiotemporal pattern of the El Niño climate phenomenon over the tropical Pacific, rather than treats them as separated and isolated branches of mathematics and statistics. This integrated approach empowers undergraduate students to be competitive in the job market. Many existing mathematical modeling books are built on differential equation models, either ordinary differential equation or partial differential equation, and thus involve techniques of solving differential equations, either analytically or numerically. Those books require the background knowledge of Calculus II or III or more advanced mathematics, and are for senior or graduate levels in mathematics physics or engineering. Our book is different and the course of differential equations is not a prerequisite. Instead, this book emphasizes the current and future needs of mathematical modeling based on real data and computer programming, and includes practical tools of linear regression, stochastic modeling, and machine learning.
Another feature of this book is to show students how to write short proposals and consulting reports based on mathematical modeling approaches. We emphasize problemsolving and product development through elucidating the modeling objectives and results interpretation, in addition to the model development and solutions. This process helps train students to pursue or create excellent jobs of mathematical consulting, a career similar to but different from the popular statistical consulting.